对平衡树的研究与探索

[TOC]

【摘要】

本文较全面地介绍了各种常用平衡树及其特点，复杂度和实用性。

第一部分提出各种不同的二叉搜索树的性质、性能、实现方法、模板。第二部分主要介绍了可持久化treap。第三部分详细地对各种平衡树进行实战比较。

【关键字】二叉搜索树 treap splay sbt rbt 替罪羊树 AVL

【正文】

一、引言

	 平衡树在信息学竞赛中十分常见，作为较易实现各种功能以及自己自身的特有的代码短、时间优的特点，占据了信息学竞赛的至少30%的数据结构考点。平衡二叉树（Balanced Binary Tree）具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树（rbt）、AVL、替罪羊树、Treap、伸展树（spaly）平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

二、各类平衡树的基本介绍

平衡二叉树

一个长度为n的有序序列，从中查找一个指定的值，要花多少时间？一个最简单的做法就是一个个去试。如果你运气好，第一个就碰上了；如果你运气不好，最后一个才是你要查的值，那就需要把n个值都检查一遍。时间复杂度O(n)。当然你可能注意到了有序这个有用的性质，所以可以采用二分查找的方式，具体就不赘述了。时间复杂度O(log(n))。但是如果要添加一个数据（及动态更新）怎么办？要保证序列的有序性，你必须要插入到适当的位置。这个位置同样可以通过二分查找在O(log(n))的时间中找出。可是插入的过程呢？我们必须把后面的数据一个个顺次往后挪一格，而这需要O(n)的时间。这也意味着删除的时间复杂度也就是O（n）。太慢了！无法满足大数据底线O（nlogn）左右的时间复杂度。所以我们需要快一点的方法（数据结构）。

treap

基本介绍

    树堆，在数据结构中也称Treap，是指有一个随机附加域满足堆的性质的二叉搜索树，其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树，Treap的特点是实现简单，且能基本实现随机平衡的结构。
    Treap=Tree+Heap
	Treap是一棵二叉排序树，它的左子树和右子树分别是一个Treap，和一般的二叉排序树不同的是，Treap纪录一个额外的数据，就是优先级。Treap在以关键码构成二叉排序树的同时，还满足堆的性质(在这里我们假设节点的优先级大于该节点的孩子的优先级)。但是这里要注意的是Treap和二叉堆有一点不同，就是二叉堆必须是完全二叉树，而Treap可以并不一定是。

补充

替代rand（）

对于现在的treap，附加域往往还会选用另一种方法——选用以下代码

inline int random(){
    static int seed=703; //seed可以随便取
    return seed=int(seed*48271LL%2147483647);
}

	以上就可以取遍2147483647中每一个数，对于rand（）的可能重复附加域的情况有效地排除了

可持久化

支持部分可持久化功能，详细信息见可持久化模块。

核心的步骤

旋转

	事实上，想要一棵树恰巧满足以上的条件并不容易。绝大多数情况下，我们都需要通过旋转的方法来调整树的形态，使得它满足以上的条件。 
	旋转分左旋和右旋两种，他们都不破坏二叉查找树的性质。如图所示：

这里写图片描述

插入、删除和选择第k小项

	插入和普通的二叉查找树差不多。但是要注意，插入有可能会破坏Treap的堆性质，所以要通过旋转来维护堆性质。下图就是一个例子：

这里写图片描述

	删除就相对容易很多了，由于Treap满足堆性质，只需要将待删除的节点旋转到叶子节点再删除就可以了。

操作及模板

以下代码来自黄学长（hzwer）

支持以下操作

插入x数
删除x数(若有多个相同的数，因只删除一个)
查询x数的排名(若有多个相同的数，因输出最小的排名)
查询排名为x的数
求x的前驱(前驱定义为小于x，且最大的数)

求x的后继(后继定义为大于x，且最小的数)

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
struct data{
    int l,r,v,size,rnd,w;
}tr[100005];
int n,size,root,ans;
void update(int k)//更新结点信息
{
    tr[k].size=tr[tr[k].l].size+tr[tr[k].r].size+tr[k].w;
}
void rturn(int &k)
{
    int t=tr[k].l;tr[k].l=tr[t].r;tr[t].r=k;
    tr[t].size=tr[k].size;update(k);k=t;
}
void lturn(int &k)
{
    int t=tr[k].r;tr[k].r=tr[t].l;tr[t].l=k;
    tr[t].size=tr[k].size;update(k);k=t;
}
void insert(int &k,int x)
{
    if(k==0)
    {
        size++;k=size;
        tr[k].size=tr[k].w=1;tr[k].v=x;tr[k].rnd=rand();
        return;
    }
    tr[k].size++;
    if(tr[k].v==x)tr[k].w++;
    else if(x>tr[k].v)
    {
        insert(tr[k].r,x);
        if(tr[tr[k].r].rnd<tr[k].rnd)lturn(k);
    }
    else 
    {
        insert(tr[k].l,x);
        if(tr[tr[k].l].rnd<tr[k].rnd)rturn(k);
    } 
}
void del(int &k,int x)
{
    if(k==0)return; 
    if(tr[k].v==x)
    {
        if(tr[k].w>1)
        {
            tr[k].w--;tr[k].size--;return;
        }
        if(tr[k].l*tr[k].r==0)k=tr[k].l+tr[k].r;
        else if(tr[tr[k].l].rnd<tr[tr[k].r].rnd)
            rturn(k),del(k,x);
        else lturn(k),del(k,x);
    }
    else if(x>tr[k].v)
        tr[k].size--,del(tr[k].r,x);
    else tr[k].size--,del(tr[k].l,x);
}
int query_rank(int k,int x)
{
    if(k==0)return 0;
    if(tr[k].v==x)return tr[tr[k].l].size+1;
    else if(x>tr[k].v)
        return tr[tr[k].l].size+tr[k].w+query_rank(tr[k].r,x);
    else return query_rank(tr[k].l,x);
}
int query_num(int k,int x)
{
    if(k==0)return 0;
    if(x<=tr[tr[k].l].size)
        return query_num(tr[k].l,x);
    else if(x>tr[tr[k].l].size+tr[k].w)
        return query_num(tr[k].r,x-tr[tr[k].l].size-tr[k].w);
    else return tr[k].v;
}
void query_pro(int k,int x)
{
    if(k==0)return;
    if(tr[k].v<x)
    {
        ans=k;query_pro(tr[k].r,x);
    }
    else query_pro(tr[k].l,x);
}
void query_sub(int k,int x)
{
    if(k==0)return;
    if(tr[k].v>x)
    {
        ans=k;query_sub(tr[k].l,x);
    }
    else query_sub(tr[k].r,x);
}
int main()
{
    scanf("%d",&n);
    int opt,x;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&opt,&x);
        switch(opt)
        {
        case 1:insert(root,x);break;
        case 2:del(root,x);break;
        case 3:printf("%d\n",query_rank(root,x));break;
        case 4:printf("%d\n",query_num(root,x));break;
        case 5:ans=0;query_pro(root,x);printf("%d\n",tr[ans].v);break;
        case 6:ans=0;query_sub(root,x);printf("%d\n",tr[ans].v);break;
        }
    }
    return 0;
}

sbt(节点大小平衡树)

基本介绍

	它是由中国广东中山纪念中学的陈启峰发明的。陈启峰于2006年底完成论文《Size Balanced Tree》，并在2007年的全国青少年信息学奥林匹克竞赛冬令营中发表。相比红黑树、AVL树等自平衡二叉查找树，SBT更易于实现。据陈启峰在论文中称，SBT是“目前为止速度最快的高级二叉搜索树”。SBT能在O(log n)的时间内完成所有二叉搜索树(BST)的相关操作，而与普通二叉搜索树相比，SBT仅仅加入了简洁的核心操作Maintain。由于SBT赖以保持平衡的是size域而不是其他“无用”的域，它可以很方便地实现动态顺序统计中的select和rank操作。
	由于普通sbt在实用中很频繁，所以本文重点介绍另一种在竞赛条件下可能更快的退化版sbt。

补充

与标准版的比较

标准版SBT	退化版SBT
平衡方式：Maintain	平衡方式：Maintain
	If s[left[left[t]]]>s[right[t]]
	right_rotate(t);
	If s[right[right[t]]]>s[left[t]]
	left_rotate(t);
特点：相对SPLAY,AVL,TREAP速度很快，代码短，不会退化，保证深度非常小。	特点：相对标准版SBT速度更快，代码更短，随机、有序数据不会退化（除人字形数据），深度也很小。
适用范围：任何程序中。	使用范围：在信息学竞赛中很实用，因为不太可能有人字型数据。但在实际应用中就不能保证一定不退化。

插入人字形数据后退化的SBT

这里写图片描述

模板

//标准版
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <climits>//形如INT_MAX一类的
#define MAX 111111
#define INF 0x7FFFFFFF
#define REP(i,s,t) for(int i=(s);i<=(t);++i)
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define mp(a,b) make_pair(a,b)
#define L(x) x<<1
#define R(x) x<<1|1
# define eps 1e-5
//#pragma comment(linker, "/STACK:36777216") ///传说中的外挂
using namespace std;
struct sbt {
    int l,r,s,key;
} tr[MAX];
int top , root;
void left_rot(int &x) {
    int y = tr[x].r;
    tr[x].r = tr[y].l;
    tr[y].l = x;
    tr[y].s = tr[x].s; //转上去的节点数量为先前此处节点的size
    tr[x].s = tr[tr[x].l].s + tr[tr[x].r].s + 1;
    x = y;
}
void right_rot(int &x) {
    int y = tr[x].l;
    tr[x].l = tr[y].r;
    tr[y].r = x;
    tr[y].s = tr[x].s;
    tr[x].s = tr[tr[x].l].s + tr[tr[x].r].s + 1;
    x = y;
}
void maintain(int &x,bool flag) {
    if(flag == 0) { //左边
        if(tr[tr[tr[x].l].l].s > tr[tr[x].r].s) {//左孩子左子树size大于右孩子size
            right_rot(x);
        } else if(tr[tr[tr[x].l].r].s > tr[tr[x].r].s) {//左孩子右子树size大于右孩子size
            left_rot(tr[x].l);
            right_rot(x);
        } else return ;
    } else { //右边
        if(tr[tr[tr[x].r].r].s > tr[tr[x].l].s) { //右孩子的右子树大于左孩子
            left_rot(x);
        } else if(tr[tr[tr[x].r].l].s > tr[tr[x].l].s) { //右孩子的左子树大于左孩子
            right_rot(tr[x].r);
            left_rot(x);
        } else return ;
    }
    maintain(tr[x].l,0);
    maintain(tr[x].r,1);
}
void insert(int &x,int key) {
    if(x == 0) { //空节点
        x = ++ top;
        tr[x].l = tr[x].r = 0;
        tr[x].s = 1;
        tr[x].key = key;
    } else {
        tr[x].s ++;
        if(key < tr[x].key) insert(tr[x].l,key);
        else insert(tr[x].r,key);
        maintain(x,key >= tr[x].key);
    }
}
int del(int &p,int w) {
    if (tr[p].key==w || (tr[p].l == 0 && w < tr[p].key) || (tr[p].r == 0 && w > tr[p].key)) {
        int delnum = tr[p].key;
        if (tr[p].l == 0 || tr[p].r == 0) p = tr[p].l + tr[p].r;
        else tr[p].key=del(tr[p].l,INF);
        return delnum;
    }
    if (w < tr[p].key) return del(tr[p].l,w);
    else return del(tr[p].r,w);
}
int remove(int &x,int key) {
    int k;
    tr[x].s --;
    if(key == tr[x].key || (key < tr[x].key && tr[x].l == 0) || (key > tr[x].key && tr[x].r == 0)) {
        k = tr[x].key;
        if(tr[x].l && tr[x].r) {
            tr[x].key = remove(tr[x].l,tr[x].key + 1);
        } else {
            x = tr[x].l + tr[x].r;
        }
    } else if(key > tr[x].key) {
        k = remove(tr[x].r,key);
    } else if(key < tr[x].key) {
        k = remove(tr[x].l,key);
    }
    return k;
}
int getmin() { //二叉搜索树找最小值
    int x;
    for(x = root; tr[x].l; x = tr[x].l) ;
    return tr[x].key;
}
int getmax() {
    int x;
    for(x = root ; tr[x].r; x = tr[x].r) ;
    return tr[x].key;
}
int pred(int &x,int y,int key)
//前驱 小于
{
    if(x == 0) return y;
    if(tr[x].key < key)//加上等号，就是小于等于
        return pred(tr[x].r,x,key);
    else return pred(tr[x].l,y,key);
}//pred(root,0,key)
int succ(int &x,int y,int key) { //后继 大于
    if(x == 0) return y;
    if(tr[x].key > key)
        return succ(tr[x].l,x,key);
    else return succ(tr[x].r,y,key);
}
int select(int &x,int k) { //求第k小数
    int r = tr[tr[x].l].s + 1;
    if(r == k) return tr[x].key;
    else if(r < k) return select(tr[x].r,k - r);
    else return select(tr[x].l,k);
}
int rank(int &x,int key) { //求第K小数的逆运算
    if(key < tr[x].key) return rank(tr[x].l,key);
    else if(key > tr[x].key) return rank(tr[x].r,key);
    else return tr[tr[x].l].s + 1;
}
void inorder(int &x) {
    if(x == 0) return;
    else {
        inorder(tr[x].l);
        cout<< x <<" "<< tr[x].key << " " <<tr[x].s << " " <<tr[tr[x].l].key << " " << tr[tr[x].r].key << endl;
        inorder(tr[x].r);
    }
}

//This is a degenerated but fast version.（退化版）
#include<iostream>
#define sz(t) (t==NULL?0:t->s)
using namespace std;
struct Node{
	int key,s;
	Node *left,*right;
	Node(int a):s(1),left(NULL),right(NULL),key(a){}	
};
int cmp(Node *a,Node *b){
	return a->key-b->key;
}
void update(Node *t){
	if(!t)
		return;
	t->s=sz(t->left)+sz(t->right)+1;
}
void rr(Node *&t,Node *k){
	t->left=k->right;
	k->right=t;
	update(t);
	update(k);
	t=k;
}
void lr(Node *&t,Node *k){
	t->right=k->left;
	k->left=t;
	update(t);
	update(k);
	t=k;
}
void insert(Node *&t,Node *k){
	if(t==NULL)
		t=k;
	else
		if(cmp(k,t)<0){
			insert(t->left,k);
			if(sz(t->left->left)>sz(t->right))
				rr(t,t->left);
		}
		else{
			insert(t->right,k);
			if(sz(t->right->right)>sz(t->left))
				lr(t,t->right);
		}
	update(t);
}
Node findmin(Node *t){
	while(t->left!=NULL)
		t=t->left;
	return *t;
}
void remove(Node *&t,Node *k){
	if(t==NULL)
		return;
	if(cmp(k,t)==0)
		if(t->right==NULL){
			k=t->left;
			delete t;
			t=k;
		}
		else{
			Node tmp=findmin(t->right);
			remove(t->right,&tmp);
			tmp.left=t->left;
			tmp.right=t->right;
			*t=tmp;
		}
	else
		if(cmp(k,t)<0)
			remove(t->left,k);
		else
			remove(t->right,k);
	update(t);
}
void preorder(Node *t){
	if(t==NULL)
		return;
	preorder(t->left);
	printf("%d ",t->key);
	preorder(t->right);
}
int main(){
}

splay

基本介绍

伸展树（Splay Tree），也叫分裂树，是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造，后勃刚对其进行了改进。它的优势在于不需要记录用于平衡树的冗余信息。在伸展树上的一般操作都基于伸展操作。创造者是Daniel Sleator和Robert Tarjan。优点有每次查询会调整树的结构，使被查询频率高的条目更靠近树根。

实现操作

Tree Rotation 这里写图片描述树的旋转是splay的基础，对于二叉查找树来说，树的旋转不破坏查找树的结构。 Splaying Splaying是Splay Tree中的基本操作，为了让被查询的条目更接近树根，Splay Tree使用了树的旋转操作，同时保证二叉排序树的性质不变。 Splaying的操作受以下三种因素影响： 1.节点x是父节点p的左孩子还是右孩子 2.节点p是不是根节点，如果不是 3.节点p是父节点g的左孩子还是右孩子同时有三种基本操作： 1.Zig Step 这里写图片描述当p为根节点时，进行zip step操作。当x是p的左孩子时，对x右旋；当x是p的右孩子时，对x左旋。 2.Zig-Zig Step 当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。当x和p同为左孩子时，依次将p和x右旋；当x和p同为右孩子时，依次将p和x左旋。 3.Zig-Zag Step 这里写图片描述当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。当p为左孩子，x为右孩子时，将x左旋后再右旋。当p为右孩子，x为左孩子时，将x右旋后再左旋。 Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树先序遍历结果不变的特性，可以将区间按顺序建二叉查找树。

应用

每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。这样，大部分区间问题都可以很方便的解决，操作同样也适用于一个或多个条目的添加或删除，和区间的移动。

补充

splay在竞赛中有时会被写成单旋

//单旋
inline void splay(int x,int g=0){
    if(t[x].p==g)pd(x);
    else{
        while(t[x].p!=g)rot(x);
        pu(x);
    }
}

但这在有序数据下是达不到O（logn）的，试想一下如果当前是一条链的话，在查询完最深的节点后，只用N个单旋把节点单旋上去的话，splay操作后的树仍然是一条链。这里写图片描述所以要使用双选来维持二叉搜索树的平衡。

//双旋
inline void spaly(node *t, node *p) {
    while (t->father != p) {
        node *f = t->father;
        node *g = f->father;
        if (g == p)
            rotate(t);
        else {
            if (son(g, f) ^ son(f, t))
                rotate(t), rotate(t);
            else
                rotate(f), rotate(t);
        }
    }
}

序列之王

在有可持久化treap之前，动态树（LCT）几乎全由splay完成，包括各种序列操作以及文本编辑器类型的题。

//含merge与split的splay模板
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
using namespace std;
int n,m,l,r;
struct splay{
    splay *ch[2],*fa;
    int val,sz;
    bool flip;
    splay(int);
    int cmp(int k)
    {
        if(k<=ch[0]->sz)  return 0;
        if(k>ch[0]->sz+1) return 1;
        return -1;
    }
    void maintain() {sz=1+ch[0]->sz+ch[1]->sz;}
    splay* find_it(int k)
    {
        push_down();
        int d=cmp(k);
        if(d==-1) return this;
        if(d==1) k-=ch[0]->sz+1;
        return ch[d]->find_it(k);
    }
    void push_down();
}*null=new splay(0),*V,*x,*y;
splay :: splay(int x)
{
    sz=null?1:0;
    val=x;flip=false;
    ch[0]=ch[1]=fa=null;
}
void splay :: push_down()
{
    if(!flip) return;
    flip=false;
    swap(ch[0],ch[1]);
    if(ch[0]!=null) ch[0]->flip=!ch[0]->flip;
    if(ch[1]!=null) ch[1]->flip=!ch[1]->flip;
    return;
}
void turn(splay *c,int d)
{
    splay *y=c->fa;
    y->ch[d^1]=c->ch[d];
    if(c->ch[d]!=null) c->ch[d]->fa=y;
    c->ch[d]=y;
    c->fa=y->fa;
         if(y->fa->ch[0]==y) y->fa->ch[0]=c;
    else if(y->fa->ch[1]==y) y->fa->ch[1]=c;
    y->fa=c;
    y->maintain();
    c->maintain();
}
void splaying(splay *c)
{
    splay *y,*z;
    while(c->fa!=null)
    {
        y=c->fa;z=y->fa;
        int d1=y->ch[0]==c?0:1;
        if(z!=null)
        {
            int d2=z->ch[0]==y?0:1;
            if(d1==d2) turn(y,d1^1),turn(c,d1^1);
            else       turn(c,d1^1),turn(c,d1);
        }
        else turn(c,d1^1);
    }
}
void build(splay *&c,int l,int r)
{
    if(l>r) return;
    int mid=l+r>>1;
    c=new splay(mid);
    build(c->ch[0],l,mid-1);
    build(c->ch[1],mid+1,r);
    if(c->ch[0]!=null) c->ch[0]->fa=c;
    if(c->ch[1]!=null) c->ch[1]->fa=c;
    c->maintain();
    return;
}
splay* Merge(splay *x,splay *y)
{
    if(x==null) return y;
    if(y==null) return x;
    splay *c=x->find_it(x->sz);
    splaying(c);
    c->ch[1]=y;
    y->fa=c;
    c->maintain();
    return c;
}
void Split(splay *V,splay *&x,splay *&y,int k)
{
    if(k<=0)     {x=null;y=V;return;}
    if(k>=V->sz) {x=V;y=null;return;}
    splay *c=V->find_it(k);
    splaying(c);
    y=c->ch[1];y->fa=null;
    x=c;       x->ch[1]=null;
    x->maintain();
    return;
}
void cs(splay *c)
{
    if(c==null) return;
    c->push_down();
    cs(c->ch[0]);
    printf("%d ",c->val);
    cs(c->ch[1]);
    return;
}
int main()
{
    scanf("%d%d",&n,&m);
    build(V,1,n);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&l,&r);
        Split(V,V,x,l-1);
        Split(x,x,y,r-l+1);
        if(x!=null) x->flip=!x->flip;
        V=Merge(V,x);
        V=Merge(V,y);
    }
    cs(V);
    return 0;
}

RBT（红黑树）

这是一个在当今信息界公认的最快的平衡二叉树之一!!!STL里的< set >与< map >就由其作为底层数据结构 这里写图片描述

基本介绍

红黑树（Red Black Tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。它的统计性能要好于平衡二叉树（AVL）因此，红黑树在很多地方都有应用。在C++ STL中，很多部分(包括set, multiset, map, multimap)应用了红黑树的变体(SGI STL中的红黑树有一些变化，这些修改提供了更好的性能，以及对set操作的支持。

性质

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

性质1. 节点是红色或黑色。性质2. 根节点是黑色。性质3 每个叶节点（NIL节点，空节点）是黑色的。性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点) 性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。要知道为什么这些特性确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。在很多树数据结构的表示中，一个节点有可能只有一个子节点，而叶子节点不包含数据。用这种范例表示红黑树是可能的，但是这会改变一些属性并使算法复杂。为此，本文中我们使用 "nil 叶子" 或"空(null)叶子"，如上图所示，它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略，导致了这些树好象同上述原则相矛盾，而实际上不是这样。与此有关的结论是所有节点都有两个子节点，尽管其中的一个或两个可能是空叶子。

引理

引理：一棵有n个内结点的红黑树的高度至多为2lg(n+1)。

这个引理怎么证明呢，这里需要一个工具对以x为根的子树，它所包含的内部结点数至少为2^[bh(x)]-1。这里bh(x)（bh嘛，black height）被定义为结点x的黑高度，就是说，从结点x（不包括它本身）到它任一个叶结点的路径上所有黑色结点的个数。下面用归纳法证明： 1)若x高度为0，那么它就是一叶子结点，它确实至少包含2^0-1=0个内部结点 2)假设x为红黑树的某一内部结点，且它高度h>0，那么它的黑高度就是bh(x)，但是它的两个孩子结点呢？这个就根据它们的颜色来判断了：如果x有一个红色的孩子y，那么y的黑高度bh(y)=bh(x)，看看上面对黑高度的定义你就明白了——既然它是红色的，那么它的黑高度就应该和它父亲的黑高度是一样的；如果x有一个黑色的孩子z，那么z的黑高度bh(z)=bh(x)-1，这个怎么解释呢，因为它自己就是个黑结点，那么在计算它的黑高度时，必须把它自己排除在外（还是根据定义），所以它是bh(x)-1。 3)x的孩子结点所构成的子树的高度肯定小于x这颗子树，那么对于这两个孩子，不管它们颜色如何，一定满足归纳假设的是至少hb 高度为bh(x)-1。所以，对x来说，它所包含的内部结点个数“至少”为两个孩子结点所包含的内部结点数，再加上它自己，于是就为2^[bh(x)-1]-1+2^[bh(x)-1]-1+1=2^[bh(x)]-1，归纳证明完毕。也就是说n>=2^[bh(x)]-1---------① 把一中红黑树性质中 4）、5）两个特性结合起来，其实我们可以得到黑节点至少是红节点的2倍。用一句话来说就是“有红必有黑，但有黑未必一定有红”。为什么这么说呢，因为从特性4）我们知道，如果有一个红结点存在，那么它的儿子结点一定是黑的，最极端的情况下，该路径上所有的结点就被红、黑两种结点给平分了那就是黑节点至少是红节点的2倍。不知这个问题我解释清楚没有，因为这是往下理解的关键。如果一棵红黑树的高为h，那么在这个高度上（不包括根结点本身）至少有1/2h的黑结点，再结合上面对“黑高度”的定义，我们说，红黑树根结点的黑高度至少是1/2h，好了，我们拿出公式①，设n为该红黑树所包含的内部结点数，我们得出如下结论： n>=2^(1/2h)-1。我们把它整理整理，就得到了h<=2lg(n+1)，就是我们要证明的结论：红黑树的高度最多也就是2lg(n+1)。

补充与模板

由于红黑树有5种插入、6种删除情况，而篇幅有限所以就不讨论其实现方式。下面是一篇红黑树的简介代码，可以参考实现方式。

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cstdio>
#include<vector>
#include<ctime>
const int Max_N = 110000;
struct Node {
    int data, s, c;
    bool color;
    Node *fa, *ch[2];
    inline void set(int _v, bool _color, int i, Node *p) {
        data = _v, color = _color, s = c = i;
        fa = ch[0] = ch[1] = p;
    }
    inline void push_up() {
        s = ch[0]->s + ch[1]->s + c;
    }
    inline void push_down() {
        for (Node *x = this; x->s; x = x->fa) x->s--;
    }
    inline int cmp(int v) const {
        return data == v ? -1 : v > data;
    }
};
struct RedBlackTree {
    int top;
    Node *root, *null;
    Node stack[Max_N], *tail, *store[Max_N];
    void init() {
        tail = &stack[0];
        null = tail++;
        null->set(0, 0, 0, NULL);
        root = null;
        top = 0;
    }
    inline Node *newNode(int v) {
        Node *p = null;
        if (!top) p = tail++;
        else p = store[--top];
        p->set(v, 1, 1, null);
        return p;
    }
    inline void rotate(Node* &x, bool d ) {
        Node *y = x->ch[!d];
        x->ch[!d] = y->ch[d];
        if (y->ch[d]->s) y->ch[d]->fa = x;
        y->fa = x->fa;
        if (!x->fa->s) root = y;
        else x->fa->ch[x->fa->ch[0] != x] = y;
        y->ch[d] = x;
        x->fa = y;
        y->s = x->s;
        x->push_up();
    }
    inline void insert(int v) {
        Node *x = root, *y = null;
        while (x->s) {
            x->s++, y = x;    
            int d = x->cmp(v);
            if (-1 == d) {
                x->c++;
                return;
            }
            x = x->ch[d];
        }
        x = newNode(v);
        if (y->s) y->ch[v > y->data] = x;
        else root = x;
        x->fa = y;
        insert_fix(x);
    }
    inline void insert_fix(Node* &x) {
        while (x->fa->color) {
            Node *par = x->fa, *Gp = par->fa;
            bool d = par == Gp->ch[0];
            Node *uncle = Gp->ch[d];
            if (uncle->color) {
                par->color = uncle->color = 0;
                Gp->color = 1;
                x = Gp;
            } else if (x == par->ch[d]) {
                rotate(x = par, !d);
            } else {
                Gp->color = 1;
                par->color = 0;
                rotate(Gp, d);
            }
        }
        root->color = 0;
    }
    inline Node *find(Node *x, int data) {
        while (x->s && x->data != data) x = x->ch[x->data < data];
        return x;
    }
    inline void del_fix(Node* &x) {
        while (x != root && !x->color) {
            bool d = x == x->fa->ch[0];
            Node *par = x->fa, *sibling = par->ch[d];
            if (sibling->color) {
                sibling->color = 0;
                par->color = 1;
                rotate(x->fa, !d);
                sibling = par->ch[d];
            } else if (!sibling->ch[0]->color && !sibling->ch[1]->color) {
                sibling->color = 1, x = par;
            } else {
                if (!sibling->ch[d]->color) {
                    sibling->ch[!d]->color = 0;
                    sibling->color = 1;
                    rotate(sibling, d);
                    sibling = par->ch[d];
                }
                sibling->color = par->color;
                sibling->ch[d]->color = par->color = 0;
                rotate(par, !d);
                break;
            }
        }
        x->color = 0;
    }
    inline void del(int data) {
        Node *z = find(root, data);
        if (!z->s) return;
        if (z->c > 1) {        
            z->c--;
            z->push_down();
            return;
        }
        Node *y = z, *x = null;
        if (z->ch[0]->s && z->ch[1]->s) {
            y = z->ch[1];
            while (y->ch[0]->s) y = y->ch[0];
        }
        x = y->ch[!y->ch[0]->s];
        x->fa = y->fa;
        if (!y->fa->s) root = x;
        else y->fa->ch[y->fa->ch[1] == y] = x;
        if (z != y) z->data = y->data, z->c = y->c;
        y->fa->push_down();
        for (Node *k = y->fa; y->c > 1 && k->s && k != z; k = k->fa) k->s -= y->c - 1;
        if (!y->color) del_fix(x);
        store[top++] = y;
    }
    inline void kth(int k) {
        int t;
        Node *x = root;
        for (; x->s;) {
            t = x->ch[0]->s;
            if (k <= t) x = x->ch[0];
            else if (t + 1 <= k && k <= t + x->c) break;
            else k -= t + x->c, x = x->ch[1];
        }
        printf("%d\n", x->data);
    }
    inline void rank(int v) {
        int t, cur = 0;
        Node *x = root;
        for (; x->s;) {
            t = x->ch[0]->s;
            if (v == x->data) break;
            else if (v < x->data) x = x->ch[0];
            else cur += t + x->c, x = x->ch[1];
        }
        printf("%d\n", cur + t + 1);
    }
    inline void succ(int v) {
        int ret = 0;
        Node *x = root;
        while (x->s) {
            if (x->data > v) ret = x->data, x = x->ch[0];
            else x = x->ch[1];
        }
        printf("%d\n", ret);
    }
    inline void pred(int v) {
        int ret = 0;
        Node *x = root;
        while (x->s) {
            if (x->data < v) ret = x->data, x = x->ch[1];
            else x = x->ch[0];
        }
        printf("%d\n", ret);
    }
}rbt;
int main() {
    rbt.init();
    int n, op, v;
    scanf("%d", &n);
    while (n--) {
        scanf("%d %d", &op, &v);
        if (1 == op) rbt.insert(v);
        else if (2 == op) rbt.del(v);
        else if (3 == op) rbt.rank(v);
        else if (4 == op) rbt.kth(v);
        else if (5 == op) rbt.pred(v);
        else rbt.succ(v);
    }
    return 0;
}

AVL树-二叉查找树

基本介绍

AVL在计算机科学中是最先发明的自平衡二叉查找树。AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis，他们在 1962 年的论文《An algorithm for the organization of information》中发表了它。

计算节点

高度为 h 的 AVL 树，节点数 N 最多2^h − 1；最少（其中）。最少节点数 n 如以斐波那契数列可以用数学归纳法证明： Nh=F【h+ 2】 - 1 (F【h+ 2】是 Fibonacci polynomial 的第h+2个数）。即： N0 = 0 （表示 AVL Tree 高度为0的节点总数） N1 = 1 （表示 AVL Tree 高度为1的节点总数） N2 = 2 （表示 AVL Tree 高度为2的节点总数） Nh=N【h− 1】 +N【h− 2】 + 1 （表示 AVL Tree 高度为h的节点总数）换句话说，当节点数为 N 时，高度 h 最多为节点的平衡因子是它的右子树的高度减去它的左子树的高度。带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

操作

AVL树的基本操作一般涉及运做同在不平衡的二叉查找树所运做的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL 旋转"。假设由于在二叉排序树上插入结点而失去平衡的最小子树根结点的指针为a（即a是离插入点最近，且平衡因子绝对值超过1的祖先结点），则失去平衡后进行进行的规律可归纳为下列四种情况：单向右旋平衡处理RR：由于在a的左子树根结点的左子树上插入结点，a的平衡因子由1增至2，致使以a为根的子树失去平衡，则需进行一次右旋转操作；单向左旋平衡处理LL：由于在a的右子树根结点的右子树上插入结点，a的平衡因子由-1变为-2，致使以a为根的子树失去平衡，则需进行一次左旋转操作；双向旋转（先左后右）平衡处理LR：由于在a的左子树根结点的右子树上插入结点，a的平衡因子由1增至2，致使以a为根的子树失去平衡，则需进行两次旋转（先左旋后右旋）操作。双向旋转（先右后左）平衡处理RL：由于在a的右子树根结点的左子树上插入结点，a的平衡因子由-1变为-2，致使以a为根的子树失去平衡，则需进行两次旋转（先右旋后左旋）操作。其他操作与其他平衡树类似。此数据结构插入、查找和删除的时间复杂度均为O(logN)，但是插入和删除需要额外的旋转算法需要的时间，有时旋转过多也会影响效率。

完整模板

/***********
*AvlTree.h*
***********/
#include <iostream>
template<typename Comparable>
class AvlTree {
public:
    AvlTree() {
        root = NULL;
    } // Constructor
    AvlTree(const AvlTree & rhs) {
        root = NULL;
        *this = rhs;
    } // Copy Constructor
    const AvlTree & operator=(const AvlTree & rhs) {
        if (this != &rhs) {
            makeEmpty();
            root = clone(rhs.root);
        }
        return *this;
    } // Overload "operator="
    ~AvlTree() {
        makeEmpty();
    } // Destructor
    const Comparable & findMin() const {
        return findMin(root);
    } // Find Minimum Element
    const Comparable & findMax() const {
        return findMax(root);
    } // Find Maximum Element
    bool contains(const Comparable & x) const {
        return contains(x, root);
    } // Test if an item is in the tree.
    bool isEmpty() const {
        return root == NULL;
    } // Test if the tree is empty.
    void makeEmpty() {
        makeEmpty(root);
    } // Make the tree empty.
    void insert(const Comparable & x) {
        insert(x, root);
    } // Insert an item into the tree.
    void remove(const Comparable & x) {
        remove(x, root);
    } // Remove an item from the tree.
    void printTree(std::ostream & out = std::cout) const {
        if (isEmpty())
            out << "Empty Tree" << std::endl;
        else
            printTree(root, out);
    } // Print the tree in sorted order.
    int treeHeight() const {
        return treeHeight(root);
    } // Compute the height of the tree.
private:
    struct AvlNode {
        Comparable element;
        AvlNode *left;
        AvlNode *right;
        int height;
        AvlNode(const Comparable & theElement, AvlNode *lt, AvlNode *rt, int h = 0) : element(theElement), left(lt), right(rt), height(h) {}
    };
    AvlNode *root;
    void insert(const Comparable & x, AvlNode * & t);
    void remove(const Comparable & x, AvlNode * & t);
    AvlNode * findMin(AvlNode *t) const;
    AvlNode * findMax(AvlNode *t) const;
    bool contains(const Comparable & x, AvlNode *t) const;
    void makeEmpty(AvlNode * & t);
    void printTree(AvlNode *t, std::ostream & out) const;
    int treeHeight(AvlNode *t) const;
    AvlNode * clone(AvlNode *t) const;
    int height(AvlNode *t) const;
    void rotateWithLeftChild(AvlNode * & k2);
    void rotateWithRightChild(AvlNode * & k2);
    void doubleWithLeftChild(AvlNode * & k3);
    void doubleWithRightChild(AvlNode * & k3);
}
;

/*************
*AvlTree.cpp*
*************/
#include "AvlTree.h"
template<typename Comparable>
typename AvlTree<Comparable>::AvlNode * AvlTree<Comparable>::findMin(
        AvlNode *t) const {
    if (t == NULL)
        return NULL;
    if (t->left == NULL)
        return t;
    return findMin(t->left);
}
template<typename Comparable>
typename AvlTree<Comparable>::AvlNode * AvlTree<Comparable>::findMax(
        AvlNode *t) const {
    if (t == NULL)
        return NULL;
    if (t->right == NULL)
        return t;
    return findMax(t->left);
}
/**
* Internal method to test if an item is in a subtree.
* x is item to search for.
* t is the node that roots the subtree.
*/
template<typename Comparable>
bool AvlTree<Comparable>::contains(const Comparable & x, AvlNode *t) const {
    if (t == NULL)
        return false;
    else if (t->element > x)
        return contains(x, t->left);
    else if (x > t->element)
        return contains(x, t->right);
    else
        return true; // Match
}
/**
* Internal method to insert into a subtree.
* x is the item to insert.
* t is the node that roots the subtree.
* Set the new root of the subtree.
*/
template<typename Comparable>
void AvlTree<Comparable>::insert(const Comparable & x, AvlNode * & t) {
    if (t == NULL)
        t = new AvlNode(x, NULL, NULL);
    else if (t->element > x) {
        insert(x, t->left);
        if (height(t->left) - height(t->right) == 2) {
            if (t->left->element > x)
                rotateWithLeftChild(t);
            else
                doubleWithLeftChild(t);
        }
    } else if (x > t->element) {
        insert(x, t->right);
        if (height(t->right) - height(t->left) == 2) {
            if (x > t->right->element)
                rotateWithRightChild(t);
            else
                doubleWithRightChild(t);
        }
    } else
        ; // Duplicate; do nothing
    t->height = std::max(height(t->left), height(t->right)) + 1;
}
/**
* Internal method to remove from a subtree.
* x is the item to remove.
* t is the node that roots the subtree.
* Set the new root of the subtree.
*/
template<typename Comparable>
void AvlTree<Comparable>::remove(const Comparable & x, AvlNode * & t) {
    if (t == NULL)
        return;
    // Item not found; do nothing
    if (t->element > x) {
        remove(x, t->left);
        if (height(t->right) - height(t->left) == 2) {
            if (height(t->right->right) >= height(t->right->left))
                rotateWithRightChild(t);
            else
                doubleWithRightChild(t);
        }
    } else if (x > t->element) {
        remove(x, t->right);
        if (height(t->left) - height(t->right) == 2) {
            if (height(t->left->left) >= height(t->left->right))
                rotateWithLeftChild(t);
            else
                doubleWithLeftChild(t);
        }
    } else if (t->left != NULL && t->right != NULL) {
        t->element = findMin(t->right)->element;
        remove(t->element, t->right);
        t->height = std::max(height(t->left), height(t->right)) + 1;
    } else {
        AvlNode *oldNode = t;
        t = (t->left != NULL) ? t->left : t->right;
        delete oldNode;
    }
    if (t != NULL)
        t->height = std::max(height(t->left), height(t->right)) + 1;
}
/**
* Internal method to make subtree empty.
*/
template<typename Comparable>
void AvlTree<Comparable>::makeEmpty(AvlNode * & t) {
    if (t != NULL) {
        makeEmpty(t->left);
        makeEmpty(t->right);
        delete t;
    }
    t = NULL;
}
/**
* Internal method to clone subtree.
*/
template<typename Comparable>
typename AvlTree<Comparable>::AvlNode * AvlTree<Comparable>::clone(
        AvlNode *t) const {
    if (t == NULL)
        return NULL;
    return new AvlNode(t->element, clone(t->left), clone(t->right));
}
/**
* Internal method to print a subtree rooted at t in sorted order.
*/
template<typename Comparable>
void AvlTree<Comparable>::printTree(AvlNode *t, std::ostream & out) const {
    if (t != NULL) {
        printTree(t->left, out);
        out << t->element << ' ';
        printTree(t->right, out);
    }
}
/**
* Return the height of node t or -1 if NULL.
*/
template<typename Comparable>
int AvlTree<Comparable>::height(AvlNode *t) const {
    return t == NULL ? -1 : t->height;
}
/**
* Rotate binary tree node with left child.
* For AVL trees, this is a single rotation for case 1.
* Update heights, then set new root.
*/
template<typename Comparable>
void AvlTree<Comparable>::rotateWithLeftChild(AvlNode * & k2) {
    AvlNode *k1 = k2->left;
    k2->left = k1->right;
    k1->right = k2;
    k2->height = std::max(height(k2->left), height(k2->right)) + 1;
    k1->height = std::max(height(k1->left), k2->height) + 1;
    k2 = k1;
}
/**
* Rotate binary tree node with right child.
* For AVL trees, this is a single rotation for case 1.
* Update heights, then set new root.
*/
template<typename Comparable>
void AvlTree<Comparable>::rotateWithRightChild(AvlNode * & k2) {
    AvlNode *k1 = k2->right;
    k2->right = k1->left;
    k1->left = k2;
    k2->height = std::max(height(k2->right), height(k2->left)) + 1;
    k1->height = std::max(height(k1->right), k2->height) + 1;
    k2 = k1;
}
/**
* Double rotate binary tree node: first left child
* with its right child; then node k3 with new left child.
* For AVL trees, this is a double rotation for case 2.
* Update heights, then set new root.
*/
template<typename Comparable>
void AvlTree<Comparable>::doubleWithLeftChild(AvlNode * & k3) {
    rotateWithRightChild(k3->left);
    rotateWithLeftChild(k3);
}
/**
* Double rotate binary tree node: first right child
* with its left child; then node k3 with new right child.
* For AVL trees, this is a double rotation for case 2.
* Update heights, then set new root.
*/
template<typename Comparable>
void AvlTree<Comparable>::doubleWithRightChild(AvlNode * & k3) {
    rotateWithLeftChild(k3->right);
    rotateWithRightChild(k3);
}
/**
* Internal method to compute the height of a subtree rooted at t.
*/
template<typename Comparable>
int AvlTree<Comparable>::treeHeight(AvlNode *t) const {
    if (t == NULL)
        return -1;
    else
        return 1 + std::max(treeHeight(t->left), treeHeight(t->right));
}

/*********
*main.cpp*
**********/
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "AvlTree.cpp"
int main() {
    AvlTree<int> t1;
    srand(time(NULL));
    for (int i = 0; i < 127; i++) {
        t1.insert(rand());
    }
    std::cout << "t1's height=" << t1.treeHeight() << std::endl;
    std::cout << "t1 is { ";
    t1.printTree();
    std::cout << "}" << std::endl;
    AvlTree<int> t2(t1);
    int n = 0;
    while (n < 96) {
        int j = rand();
        if (t2.contains(j)) {
            t2.remove(j);
            n++;
        }
    }
    t1 = t2;
    std::cout << "t1's height=" << t1.treeHeight() << std::endl;
    std::cout << "t1 is { ";
    t1.printTree();
    std::cout << "}" << std::endl;
    return 1;
}

替罪羊树

基本介绍

替罪羊树是计算机科学中，一种基于部分重建的自平衡二叉搜索树。在替罪羊树上，插入或删除节点的平摊最坏时间复杂度是O(log n)，搜索节点的最坏时间复杂度是O(log n)。在非平衡的二叉搜索树中，每次操作以后检查操作路径，找到最高的满足max(size(son_L),size(son_R))>alpha*size(this)的结点，重建整个子树。这样就得到了替罪羊树，而被重建的子树的原来的根就被称为替罪羊节点。对于一棵二叉搜索树，最重要的事情就是维护他的平衡，以保证对于每次操作（插入，查找，删除）的时间均摊下来都是乃至（红黑树，但是常数大而且难写，此处不展开介绍）。为了维护树的平衡，各种平衡二叉树绞尽脑汁方法五花八门，但几乎都是通过旋转的操作来实现，只不过是在判断什么时候应该旋转上有所不同。但替罪羊树就是那么一棵特立独行的猪，哦不，是一只特立独行的树。

操作

重构

重构允许重构整棵替罪羊树，也允许重构替罪羊树其中的一棵子树。重构这个操作看似高端，实则十分暴力。主要操作就是把需要重构的子树拍平（由于子树一定是二叉搜索树，所以拍平之后的序列一定也是有序的），然后拎起序列的中点，作为根部，剩下的左半边序列为左子树，右半边序列为右子树，接着递归对左边和右边进行同样的操作，直到最后形成的树中包含的全部为点而不是序列（这样形成的一定是一棵完全二叉搜索树，也是最优的方案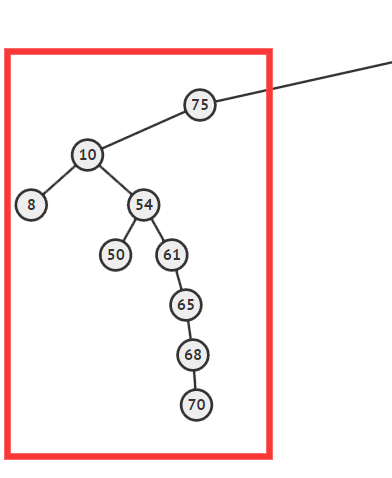）。这里写图片描述这是一棵需要维护的子树，虽然目前不知道基于什么判断条件，但这棵是明显需要维护的。拍平之后的结果，直接遍历即可。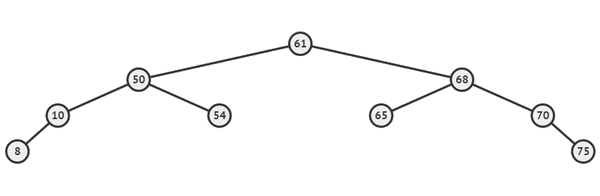子树的重构就完成了。

插入

插入操作一开始和普通的二叉搜索树无异，但在插入操作结束以后，从插入位置开始一层一层往上回溯的时候，对于每一层都进行一次判断，一直找到最后一层不满足该条件的层序号 $这里写图片描述$ （也就是从根开始的第一层不满足该条件的层序号），然后从该层开始重构以该层为根的子树（一个节点导致树的不平衡，就要导致整棵子树被拍扁，估计这也是“替罪羊”这个名字的由来吧）。每次插入操作的复杂度为 $这里写图片描述$ ，每次重构树的复杂度为 $这里写图片描述$ ，但由于不会每次都要进行重构，也不会每次都重构一整棵树，所以均摊下来的复杂度还是 $这里写图片描述$ 。 α在这里是一个常数，可以通过调整的大小来控制树的平衡度，使程序具有很好的可控性。（0.5,1）区间内α的取值对于程序性能并没有很大的影响，所以一般区0.7±0.05左右。

删除

删除操作是替罪羊树中最独特的地方，替罪羊树的删除节点并不是真正的删除，而是惰性删除（即给节点增加一个已经删除的标记，删除后的节点与普通节点无异，只是不参与查找操作而已）。当删除的数量超过树的节点数的一半时，直接重构！可以证明均摊下来的复杂度还是 $这里写图片描述$ 。

其他操作

其他操作大致相同，只需要注意一下是否标记。

代码模板

#include <vector>
using namespace std;
namespace Scapegoat_Tree {
#define MAXN (100000 + 10)
	const double alpha = 0.75;
	struct Node {
	Node * ch[2];
	int key, size, cover; // size为有效节点的数量，cover为节点总数量 
	bool exist;	// 是否存在（即是否被删除） 
	void PushUp(void) {
		size = ch[0]->size + ch[1]->size + (int)exist;
		cover = ch[0]->cover + ch[1]->cover + 1;
	}
	bool isBad(void) { // 判断是否需要重构 
		return ((ch[0]->cover > cover * alpha + 5) || 
				(ch[1]->cover > cover * alpha + 5));
		}
	};
	struct STree {
	protected:
		Node mem_poor[MAXN]; //内存池，直接分配好避免动态分配内存占用时间 
		Node *tail, *root, *null; // 用null表示NULL的指针更方便，tail为内存分配指针，root为根 
		Node *bc[MAXN]; int bc_top; // 储存被删除的节点的内存地址，分配时可以再利用这些地址 
		Node * NewNode(int key) {
			Node * p = bc_top ? bc[--bc_top] : tail++;
			p->ch[0] = p->ch[1] = null;
			p->size = p->cover = 1; p->exist = true;
			p->key = key;
			return p;
		}
		void Travel(Node * p, vector<Node *>&v) {
			if (p == null) return;
			Travel(p->ch[0], v);
			if (p->exist) v.push_back(p); // 构建序列 
			else bc[bc_top++] = p; // 回收 
			Travel(p->ch[1], v);
		}
		Node * Divide(vector<Node *>&v, int l, int r) {
			if (l >= r) return null;
			int mid = (l + r) >> 1;
			Node * p = v[mid];
			p->ch[0] = Divide(v, l, mid);
			p->ch[1] = Divide(v, mid + 1, r);
			p->PushUp(); // 自底向上维护，先维护子树 
			return p;
		}
		void Rebuild(Node * &p) {
			static vector<Node *>v; v.clear();
			Travel(p, v); p = Divide(v, 0, v.size());
		}
		Node ** Insert(Node *&p, int val) {
			if (p == null) {
				p = NewNode(val);
				return &null;
			}
			else {
				p->size++; p->cover++;
				
				// 返回值储存需要重构的位置，若子树也需要重构，本节点开始也需要重构，以本节点为根重构 
				Node ** res = Insert(p->ch[val >= p->key], val);
				if (p->isBad()) res = &p;
				return res;
			}
		}
		void Erase(Node *p, int id) {
			p->size--;
			int offset = p->ch[0]->size + p->exist;
			if (p->exist && id == offset) {
				p->exist = false;
				return;
			}
			else {
				if (id <= offset) Erase(p->ch[0], id);
				else Erase(p->ch[1], id - offset);
			}
		}
	public:
		void Init(void) {
			tail = mem_poor;
			null = tail++;
			null->ch[0] = null->ch[1] = null;
			null->cover = null->size = null->key = 0;
			root = null; bc_top = 0;
		}
		STree(void) { Init(); }
		void Insert(int val) {
			Node ** p = Insert(root, val);
			if (*p != null) Rebuild(*p);
		}
		int Rank(int val) {
			Node * now = root;
			int ans = 1;
			while (now != null) { // 非递归求排名 
				if (now->key >= val) now = now->ch[0];
				else {
					ans += now->ch[0]->size + now->exist;
					now = now->ch[1];
				}
			}
			return ans;
		}
		int Kth(int k) {
			Node * now = root;
			while (now != null) { // 非递归求第K大 
				if (now->ch[0]->size + 1 == k && now->exist) return now->key;
				else if (now->ch[0]->size >= k) now = now->ch[0];
				else k -= now->ch[0]->size + now->exist, now = now->ch[1];
			}
		}
		void Erase(int k) {
			Erase(root, Rank(k));
			if (root->size < alpha * root->cover) Rebuild(root);
		}
		void Erase_kth(int k) {
			Erase(root, k);
			if (root->size < alpha * root->cover) Rebuild(root);
		}
	};
#undef MAXN
}

基本介绍总结

到这里，6种常见平衡树的基本介绍就完毕了。

对平衡树的研究与探索

【摘要】

【关键字】 二叉搜索树 treap splay sbt rbt 替罪羊树 AVL

【正文】

一、引言

二、各类平衡树的基本介绍

平衡二叉树

treap

基本介绍

补充

替代rand（）

可持久化

核心的步骤

旋转

插入、删除和选择第k小项

操作及模板

sbt(节点大小平衡树)

基本介绍

补充

与标准版的比较

插入人字形数据后退化的SBT

模板

splay

基本介绍

实现操作

应用

补充

序列之王

RBT（红黑树）

基本介绍

性质

引理

补充与模板

AVL树-二叉查找树

基本介绍

计算节点

操作

完整模板

替罪羊树

基本介绍

操作

重构

插入

删除

其他操作

代码模板

基本介绍总结

【关键字】二叉搜索树 treap splay sbt rbt 替罪羊树 AVL